 U ovom tekstu možete videti teorijski pristup i razradu jednog sistema, radi lakšeg razumevanja praktnične izvedbe već napomenutog sistema.
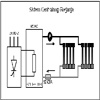
U ovom tekstu možete videti teorijski pristup i razradu jednog sistema, radi lakšeg razumevanja praktnične izvedbe već napomenutog sistema. U sistemu zatvorenog centralnog grejanja prikazanog na slici 1. potrebno je regulisati temperaturu vode. Osnova sistema je kotao sa električni grejačem. Snaga grejača je 25kW i reguliše se tiristorskim polu upravljivim ispravljačem koji je priključen na standardnu mrežu 3x380V.
Voda se greje u kotlu, krećući se na više dolazi do pumpe koja distribuira vodu radijatorima.U radijatorima se voda hladi pada naniže i vraća u kotao gde se ponovo zagreva. Senzor postavljen u povratnojgrani detektuje temperaturu vode i prosleđuje regulatoru informaciju koliko je vodu potrebno ugrejati. Zadatak regulatora je da što bržedostigne željenu temperaturu i održava je konstantnom. Ako bi usled povećanog odavanja toplote, temperatura vode u povratnoj grani opala, regulator bi povećao snagu grejača i na taj način omogućio uslove za održavanja temperature. U cilju realizacije projektnog zadatka, a to je sinteza rednog digitalnog regulatora (procesora, treba odrediti prenosnu f.-ju objekta upravljanja.
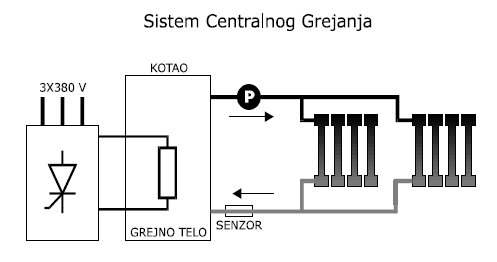
Slika 1.
Prenosana funkcija objekta upravljanja
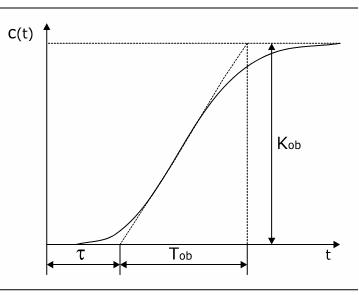
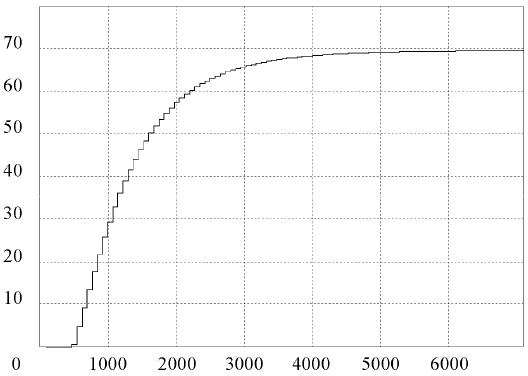
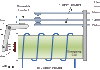
Regulacija temperatuje prostorija spada u klasi sporih industrijskih procesa. Odziv ovakvih sistema (ukoliko nije unapred poznat) se može eksperimentalno odrediti. postupak se svodi na praćenje odziva sistema koji koji je pobuđen odskočnom (Hevisajd) funkcijom. Uključenjem grejača merena je temperatura vode, a rezultat merenja je predstavljan na slici 2. Početna temperatura je bila 13oC. Grejač je priključen na maksimalni napon 380Veff. Posle t=τ=300 s temperatura se počela značajnije menjati. Nakon tih t=τob=3600 s temperatura se ustalila na 70oC.
Na osnovu ovih izmerenih podataka moguće je približno odrediti prenosnu funkciju objekta upravljanja i to u sledećem obliku:
Slika 2.
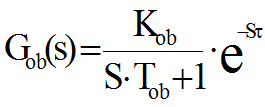
Kob – statičko pojačanje objekta,
Tob – vremenska konstanta objekta,
τ – transpotno kasnjenje objekta.
Statičko pojačanje Kob se računa prema formuli:
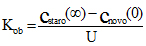
Cstaro(∞) – prvobitna(stara) stacionarna vrednost upravljane promenljive,
Cnovo(0) – nova stacionarna vrednost koja se uspostavlja,
U – amplituda pobudnog odskočnog signala.
Na osnovu ovoga dobijana vrednost Kob je:
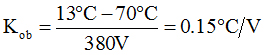
Konačno se za prenosnu funkciju objekta upravljanja dobija:
Nakon utvrđivanja prenosne funkcije objekta može se preći na projektovanje rednog digitalnog regulatora.
Struktura konture regulacije
Tipična kontura regulacije sa rednim digitalnim regulatorom prikazana je na slici 3.
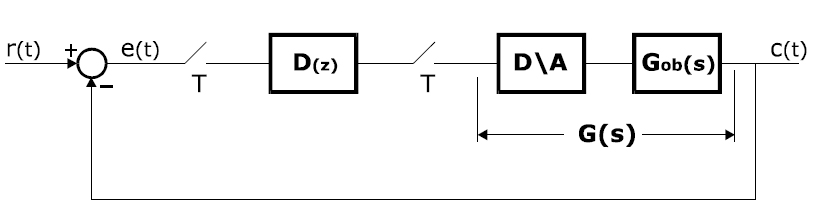
Slika 3.
Pored objekta upravljanja na blok dijagramu sa slike 3. uočavaju se sledeći objekti:
- D(z) – redni digitalni regulator – procesor
- D\A – kolo zadrške nultog reda – digitalno\analogni konvertor
Sa r(t) obeležen je referentni signal – zadata vrednost temperature od koga se oduzima c(t) – upravljana promenljiva (temperatura vode u povratnoj grani registrovana senzorom). rezultat je signal greške e(t) koji se preko odabirača, sa periodom odabiranja T, vodi na ulay regulatora D(z). Regulator – procesor u skladu sa zakonom upravljanja(programom) generiše na svom izlazu upravljačku promenljivu, digitalnu reč. Po svojoj prirodi objekat upravljanja predstavlja kontinualni deo sistema. Zato se digitalna upravljačka reč vodi preko odabirača na ulaz kola zadrške nultog reda – A\D konvertor kji na svom ulazu daje kontinualan naponski signal. na slici 3. se uočava funkcija prenosa G(s) koja je jednaka proizvodu funkcija prenosa kola zadrške i objekta upravljanja.
Prenosna funkcija kola zadrške nultog reda Gho(s) je oblika:
U ovom izrazu sa T je označena perioda odabiranja. za njeno određivanje potrebno je zadovoljiti niz strogih uslova u pogledu njene maksimalne i minimalne vrednosti. Upotrebićemo iskustvenu relaciju koja u praksi daje zadovoljavajuće rezultate:
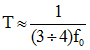
Učestalost fo označava propusni opseg sistema odnosno definiše brzinu reagovaja sistema u zatvorenoj povratnoj sprezi. Na osnovu ove relacije perioda odabiranja pa da u interval [ 75, 100 ]s, pa usvajamo T=75s .
Sada lako možemo dobiti funkciju prenosa G(s) kao:
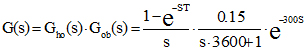
G(s) je funkcija kompleksne promenljive S. Primena Laplasove transformacije se u digitalnim sistemima bitno usložnjava. Pomenute teškoće se mogu bitno umanjiti uvođenjem Z-transformacije, koja se u osnovi svodi na zamenu:
Na ovaj način dobijamo G(z) – funkciju diskretnog prenosa:
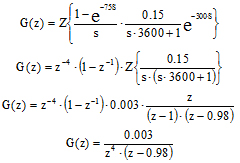
Konačni oblik konture regulacije prikazan je na slici 4.
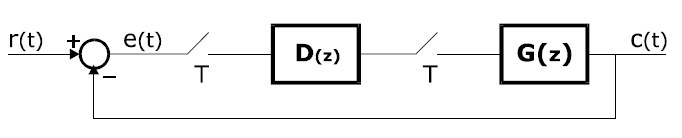
Slika 4.
Sinteza rednog digitalnog regulatora – procesora
Nakon što smo odredili diskretnu funkciju prenosa objekta upravljanja, možemo pristupiti sintezi regulatora čiji je zadatak da obezbedi zahtevane karakteristike objekta upravljanja u stacionarnom stanju. Karakter ponašanja digitalnog sistema u stacionarnom stanju određuje red astatizma sistema u odnosu na ulazni signal. Na ulazu imamo odskočni signal oblika r(t)=roh(t). Pošto je sistem bez kompenzatora nultog stepena astatizma tada će biti dovoljno dugo posle trenutaka pobude sistema, na izlazu da se uspostavi konstanta upravljanja promenljiva, ali rasaglašena sa referentnom vrednošću. pošto se zahteva da promenljiva na izlazu bude jednaka referentnoj vrednosti signala na ulazu moramo u sistem uvesti astatizam prvog reda kojeg će obezbediti proporcionalno integralni – PI regulator oblika:
U gore prikazanom zakonu upravljanja treba jo podesiti parametre proporcionalnog i integralnog dejstva Kp i Ki respektivno. Poznata Ziegler – Nicholsova procedura omogućava da se na osnovu mernih parametara u eksperimentu na sistemu sa otvorenom ili sa zatvorenom povratnom spregom odrede približno optimalne vrednosti parametara P i I dejstva. u tabeli 1 se navode parametri koji se dobijaju primenom procedure. U ppitanju su približno optimalne vrednosti parametara koje se dodatno, eksperimentalno, u postupku simulacije moraju tačnije odrediti. Za simulaciju je upotrebljen program Matlab sa svojim simulink modulom.

Tabela 1.
Primenom ove procedure dobijene su približno optimalne vrednosti parametara: kp=10.8 i ki=0.01 . Kada ove vrednosti unesemo u zakon upravljanja, simulacijom dobijamo odziv sistema na ulazni signal r(t)=roh(t) amplitude r0=70 kao na slici 5. Vidimo da je odziv sistema aperiodičan, spor i da izlaz ne dostiže zadatu vrednost dovoljno dugo nakon delovanja pobude. Menjajući parametre regulatora, simulirajući i posmatrajući odziv sistema dolazimo do vrednosti parametra pri kojima postižemo željene karakteristike stacionarnog stanja kao i dinamičkog ponašanja sistema.
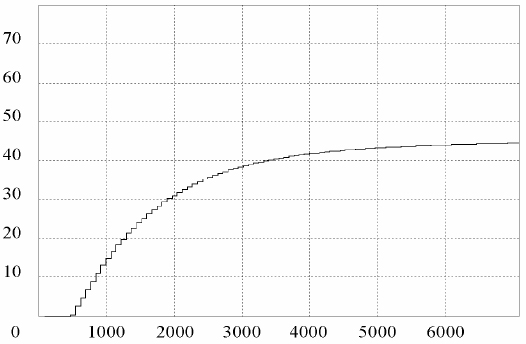
Slika 5.
Na slici 6. je prikazan odziv sistema sa PI regulatorom čiji su parametri kp=20 i ki=0.4 . Vidimo da regulisana izlazna promenljiva sistema, dostiže zadatu vrednost referentnog ulaznog signala r0=70oC. Nakon t=4000s sistem je dostigao zadatu vrednost. Odziv je relativno brz i stabilan bez prebačaja. U slučaju da se želi brži odziv javlja se značajan prebačaj što se u ovom sistemu ne sme desiti.
Slika 6.
Sinteza digitalnog P-I-D regulatora
Poboljšanje dinamičkih karaktristika, prvenstveno brzine odziva, može se postići uvođenjem diferencijalnog dejstva u zakon upravljanja. Na ovaj način dobijamo proporcionalno dintegralno diferencijalni P-I-D regulator čija je funkcija prenosa:
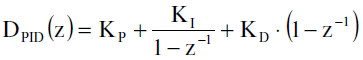
Svođenjem izraza na zajednički imenilac dobijamo funkciju prenosa oblika pogodnog za primenu u simulaciji:
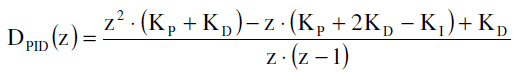
Za podešavanje P, I i D dejstva u ovom zakonu upravljanja moyemo se poslužiti eksperimentom na sistemu sa zatvorenom povratnom spregom kao na slici 7:
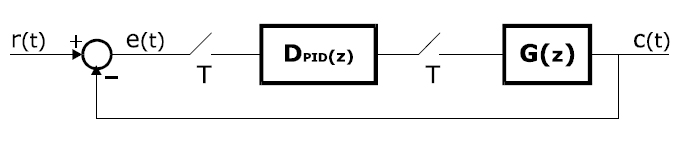
Slika 7.
Postupak se sastoji u sledećem:
Najpre se isključe I i D dejstvo postavljanjem parametara ki i kd na nulu. Pri tome se koeficijent proporcionalnog dejstva kp postavlja na neku malu vrednost pri kojoj je kuntura regulacije stabilna. Zatim se u malim iznosima povecava kp, sve dok se u nekom trenutku kontura ne nađe na oscilatorskoj granici stabilnosti. tada regulisana promenljiva c(t) u stacionarnom stanu poprima periodične oscilacije. Dostignuta vrednost kp=(kp)kr se naziva kritičnom vrednosšću pojačanja. Kritična perioda oscilocanja t=Tk , koja se pr tome javlja, predstavlja vreme između dva sukcesivna maksimamu u oscilacijama regulisane promenljive c(t).
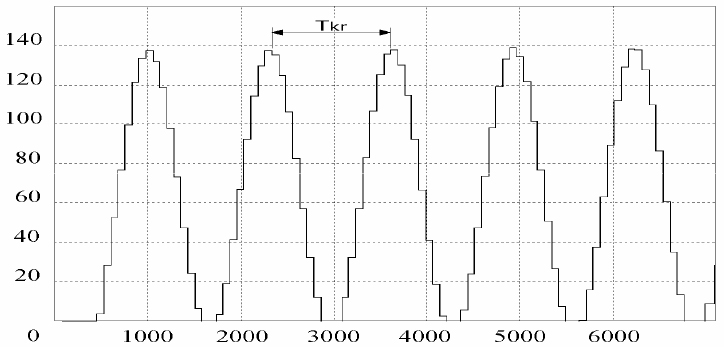
Ovim postupkom su dobijene sledeće vrednosti:
- kp=(kp)kr=120 – kritična vrednost pojačanja
- t=Tk=1250s – kritična perioda oscilovanja
Sada se na osnovu poznate Ziegler – Nicholsove procedure, predstavljene tabelom 2, određuju optimalno podešeni parametri P, I i D dejstva.

Tabela 2.
Korišteći podatke u tabeli 2, za parametre PID regulatora dobijamo:
kp=72
ki=0.0016
kd=156
Zamenjujući vrednosti koeficijenata u PID zakon upravljanja dobija se odziv kao na slici 8. Vidimo da je brzina reagovanja velika ali se uočava veliki prebačaj kao i prigučen oscilatoran odziv što je nepoželjno. Zato je neophodno dodatno podešavanje parametara. Simulacijom na računaru, posmatrajuči odziv, dobijamo optimalne vrednosti parametara navedene u daljem tekstu.
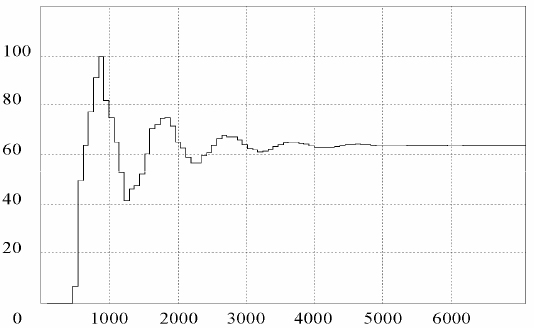
Slika 8.
Na slici 9. prikazan je odziv sistema sa PID regulatorom čiji su parametri:
kp=30
ki=0.6
kd=0.2
Sistem za t=2000s dostiže željenu vrednost i održava je konstantnom. Brzina reagovanja je duplo veća u odnosu na sistem bez diferencijalnog dejstva. Odziv je stabilan i bez prebačaja.
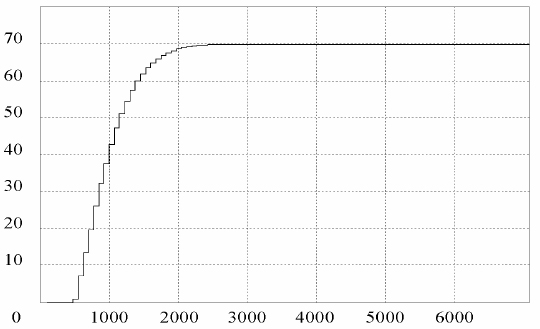
Slika 9.
Zaključak
Iz dosadašnjeg izlaganja mogu se doneti sledeći zaključci:
-
Upravljanje centralnim grejanjem spada u klasu sporih industrijskih procesa. U ovom sistemima brzina odziva nije najbitnija. Na prvom mestu su stabilnost i osustvo prebačaja regulisane promenljive. Prebačaj bi u ovakvom sistemu prouzrokovao termičko naprezanje prvenstveno kotla koji je najvažnija, a ujedno i najslabija tačka celog sistema.
-
Prenosan funkcija sistema centralnog grejanja je eksperimentalno određena uz određene aproksimacije i zanemarivanja. Usled toga su moguća veća ili manja odstupana koja će se uočiti prilikom praktične realizacije. Tu dolazi do izražaja fleksibilnost ovakvog diditalnog (mikrokontrolerskog) upravljanja. Jednostavnim izmenama softvera moguće je naknadno u praktičnoj realizaciji podesiti parametreregulatora.
-
Dobijanje stabilnog odziva koji u određenom vremenu dostiže zadatu vrednost upravljane promenljive (trmperature vode u povratnoj grani) zahteva sintezu digitalnog regulatora sa proporcionalnim i integralnim – PI dejstvom. Odziv sistema sa ovim (PI) regulatorom je relativno brz i bez prebačaja.
-
U PI uvodimo i diferencijalno D – dejstvo. Na ovaj način dobijamo digitalni PID – regulator koji u sistemu obezbeđuje brži odziv koji je stabilan i bez prebačaja.
-
Sinteza PI i PI – regulatora vršena je postupkom simulacije na računaru. Odstupanja u praktičnoj realizaciji su neizbežna ali ih je moguće korigovati.




















![Samoupravljajuće vozilo u završnoj fazi [VIDEO]](https://www.automatika.rs/wp-content/uploads/2012/03/hqdefault-5-218x150.jpg)

![EcoATM reciklira tvoj mobilni telefon i isplaćuje novac! [VIDEO] ecoatm kiosk recikliranje mobilnih telefona automatika.rs](https://www.automatika.rs/wp-content/uploads/2012/06/ecoatm_kiosk_recikliranje_mobilnih_telefona_automatika.rs.jpg)







Katastrofa nigde napišete kolko su minimalne i maximalne radne temperature i koji je optimalni pritisak za isto ovo su neki dijagrami za nekog ko treba da kao nešto studira .
U sitemu centrlnog grejanja u stamabenim zgradama u Vranju toplotnom energijom stambene zgrade snabdeva JP ,,Novi dom”Vranje. Primarni deo podstanice nije priključen prema projektovanim uslovima na režim 120/55 C, već je priključen na toplovodni kotao koji radi u mah. režim 90/70C. Da bi sa tim režimom izmenjivači imali projektovanu snagu potrebno je da protok primarnog dela bude višestruko veći od projektovanog. U primarnom delu podstanice nema automatike niti kombi ventila da bi mogao da ustanovi protok i vrši regulaciju istog. Na osnovu sagledanog stanja u primarnom delu podstanice jasno je da objekti nisu priključeni na osnovu projektovane dokumentacije. Distributer toplotne energije JP Novi Dom isporučuje enegriju na osnovu procene u odnosu na spoljnu temperaturu a ne na osnovu računske jedinice automatike koja upravlja sistemomšto je standardno za funkcionisanje sistema daljinskog grejanja. Dali li može JP Novi dom da grje 200 stanova kvaliteto sa ovakvim režimom rada.b